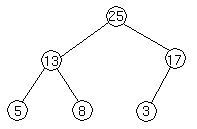
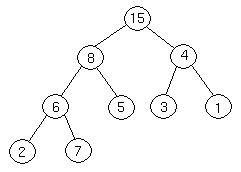
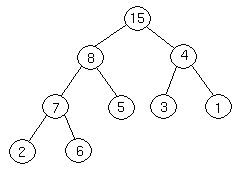
Binary Search tree is a binary tree in which each internal node x stores an element such that the element stored in the left subtree of x are less than or equal to x and elements stored in the right subtree of x are greater than or equal to x. This is called binary-search-tree property. The basic operations on a binary search tree take time proportional to the height of the tree. For a complete binary tree with node n, such operations runs in 
(lg n) worst-case time. If the tree is a linear chain of n nodes, however, the same operations takes 
(n)worst-case time.
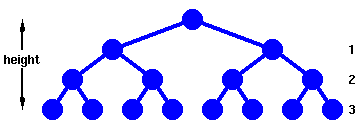
The height of the Binary Search Tree equals the number of links from the root node to the deepest node.
Implementation of Binary Search Tree
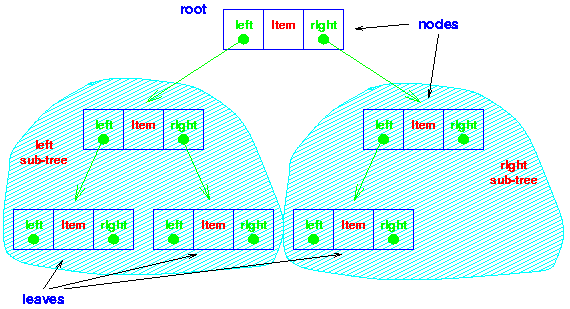
Binary Search Tree can be implemented as a linked data structure in which each node is an object with three pointer fields. The three pointer fields left, right and p point to the nodes corresponding to the left child, right child and the parent respectively NIL in any pointer field signifies that there exists no corresponding child or parent. The root node is the only node in the BTS structure with NIL in its pfield.
Inorder Tree Walk
During this type of walk, we visit the root of a subtree between the left subtree visit and right subtree visit.
INORDER-TREE-WALK(x)
If x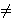 
NIL then
INORDER-TREE-WALK (left[x])
print key[x]
INORDER-TREE-WALK (right[x])
It takes (n) time to walk a tree of n nodes. Note that the Binary Search Tree property allows us to print out all the elements in the Binary Search Tree in sorted order.
Preorder Tree Walk
In which we visit the root node before the nodes in either subtree.
PREORDER-TREE-WALK(x)
If x not equal NIL then
PRINT key[x]
PREORDER-TREE-WALK (left[x])
PREORDER-TREE-WALK (right[x])
Postorder Tree Walk
In which we visit the root node after the nodes in its subtrees.
POSTORDER-TREE-WALk(x)
If x not equal NIL then
POSTORDER-TREE-WALK (left[x])
PREORDER-TREE-WALK (right[x])
PRINT key [x]
It takes O(n) time to walk (inorder, preorder and pastorder) a tree of n nodes.
Binary-Search-Tree property Vs Heap Property
In a heap, a nodes key is greater than equal to both of its children's keys. In binary search tree, a node's key is greater than or equal to its child's key but less than or equal to right child's key. Furthermore, this applies to entire subtree in the binary search tree case. It is very important to note that the heap property does not help print the nodes in sorted order because this property does not tell us in which subtree the next item is. If the heap property could used to print the keys (as we have shown above) in sorted order in O(n) time, this would contradict our known lower bound on comparison sorting.
The last statement implies that since sorting n elements takes Ω(n lg n) time in the worst case in the comparison model, any comparison-based algorithm for constructing a Binary Search Tree from arbitrary list n elements takes Ω(n lg n) time in the worst case.
We can show the validity of this argument (in case you are thinking of beating Ω(n lg n) bound) as follows: let c(n)be the worst-case running time for constructing a binary tree of a set of nelements. Given an n-node BST, the inorder walk in the tree outputs the keys in sorted order (shown above). Since the worst-case running time of any computation based sorting algorithm is Ω(n lg n) , we have
c(n) + O(n) = Ω(n lgn)
Therefore, c(n) = Ω(n lgn).
Querying a Binary Search Tree
The most common operations performed on a BST is searching for a key stored in the tree. Other operations are MINIMUM, MAXIMUM, SUCCESSOR and PREDESESSOR. These operations run in O(h) time where h is the heightof the tree i.e., h is the number of links root node to the deepest node.
The TREE-SEARCH (x, k) algorithm searches the tree root at x for a node whose key value equals k. It returns a pointer to the node if it exists otherwise NIL
TREE-SEARCH(x, k)
if x = NIL .OR. k= key[x]
then return x
if k < key[x]
then return TREE-SEARCH (left[x], k)
else return TREE-SEARCH (right[x], k)
Clearly, this algorithm runs in O(h) time where h is the height of the tree.
The iterative version of above algorithm is very easy to implement.
ITERATIVE-TREE-SEARCH(x, k)
- while x not equal NIL .AND. key ≠ key[x] do
- if k< key [x]
- then x ←left[x]
- else x ←right [x]
- return x
The TREE-MINIMUN (x) algorithm returns a point to the node of the tree at x whose key value is the minimum of all keys in the tree. Due to BST property, an minimum element can always be found by following left child pointers from the root until NIL is uncountered.
TREE-MINIMUM (x)
while left[x] ≠ NIL do
x ← left [x]
return x
Clearly, it runs in O(h) time where h is the height of the tree. Again thanks to BST property, an element in a binary search tree whose key is a maximum can always be found by following right child pointers from root until a NIL is encountered.
TREE-MAXIMUM (x)
while right[x] ≠ NIL do
x ← right [x]
return x
Clearly, it runs in O(h) time where h is the height of the tree.
The TREE-SUCCESSOR (x) algorithm returns a pointer to the node in the tree whose key value is next higher than key [x].
TREE-SUCCESSOR(x)
if right [x] ≠ NIL
then return TREE-MINIMUM (right[x])
else y ← p[x]
while y ≠ NIL .AND. x = right[y] do
x ← y
y ← p[y]
return y
Note that algorithm TREE-MINIMUM, TRE-MAXIMUM, TREE-SUCCESSOR, and TREE-PREDESSOR never look at the keys.
An inorder tree walk of an n-node BST can be implemented in (n)-time by finding the minimum element in the tree with TREE-MINIMUM (x) algorithm and then making n-1 calls to TREE-SUCCESSOR (x).
Another way of Implementing Inorder walk on Binary Search Tree
Algorithm- find the minimum element in the tree with TREE-MINIMUM
- Make n-1 calls to TREE-SUCCESSOR
Let us show that this algorithm runs in (n) time. For a tree T, let mT be the number of edges that are traversed by the above algorithm. The running time of the algorithm for T is (mT). We make following claim: mT is zero if T has at most one node and 2e - r otherwise, where e is
the number of edges in the tree and r is the length of the path from
root to the node holding the maximum key.
Note that e = n - 1 for any tree with at least one node. This allows us to prove the claim by induction on e (and therefore, on n).
Base case Suppose that e = 0. Then, either the tree is empty or consists only of a single node. So, e = r = 0. Therefore, the claim holds.
Inductive step Suppose e > 0 and assume that the claim holds for all e' < e. Let T be a binary search tree with eedges. Let x be the root, and T1 and T2 respectively be the left and right subtree of x. Since T has at least one edge, either T1 or T2 respectively is nonempty. For each i = 1, 2, let ei be the number of edges in Ti, pi the node holding the maximum key in Ti, and ri the distance from pi to the root of Ti. Similarly, let e, p and r be the correspounding values for T. First assume that both T1 and T2 are nonempty. Then e = e1 + e2 + 2, p = p2, and r = r2 + 1. The action of the enumeration is as follows: - Upon being called, the minimum-tree(x) traverses the left branch of x and enters T1.
- Once the root of T1 is visited, the edges of T1 are traversed as if T1 is the input tree. This situation will last until p1 is visisted.
- When the Tree-Successor is called form p1. The upward path from p1and x is traversed and x is discovered to hold the successor.
- When the tree-Successor called from x, the right branch of x is taken.
- Once the root of T2 is visited, the edges of T2 are traversed as if T2 is the input tree. This situation will last until p2 is reached, whereby the algorithm halts.
By the above analysis, the number of edges that are traversed by the above algorithm, mT, is mT = 1 + (2e1 - r1) + (r1 + 1) + 1 + (2e2 - r2)
= 2(e1 + e2 + 2) - (r2 + 1)
= 2e -r
Therefore, the claim clearly holds for this case.
Next suppose that T2 is emply. Since e > 0, T1 is nonempty. Then e = e1 + 1. Since x does not have a right child, x holds the maximum. Therefore, p = x and r = 0. The action of the enumeration algorithm is the first two steps. Therefore, the number of edges that are traversed by the algorithm in question is mT = 1 + (2e1 - r1) + ( r1 +1)
= 2(e1 + 1) - 0
= 2e - r
Therefore, the claim holds for this case.
Finally, assume that T1 is empty. Then T2 is nonempty. It holds that e = e2 + 1, p = p2, and r = r2 + 1. This time x holds the minimum key and the action of the enumeration algorithm is the last two steps. Therefore, the number of edges that are traversed by the algorithm is mT = 1 + (2e2 - r2)
= 2(e2+1) - (r2 + 1)
= 2e -r
Therefore, the claim holds for this case.
The claim is proven since e = n - 1, mT 
2n. On the other hand, at least one edge has to be traversed when going from on node to another, so mT 
n - 1. Therefore, the running time of the above algorithm is (n).
Consider any binary search tree T and let y be the parent of a leaf z. Our goal is to show that key[y] is either the smallest key in T larger than key[x]
or the largest key in the T smaller than key[x].
Proof Suppose that x is a left child of y. Since key[y] key[x], only we have to show that there is no node z with key[y] > key[z] > key[x]. Assume, to the contrary, that there is such a z. Choose z so that it holds the smallest key among such nodes. Note for every node u 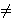z, x, key[z] dey[u] if and only if key[x] key[u]. If we search key[z], then the search path is identical to that of key[x] until the path rearches z or x. Since x is a leaf (meaning it has no children), the search path never reaches x. Therefore, z is an ancestor of x. Since y is the parent of x (it is given, in case you've forgotton!) and is not z, z has to be an ancestor of y. So, key[y] > dey[z] >dey[x]. However, we are assuming key[y] > key[z] > key[x], so this is clearly impossible. Therefore, there is no such z.
The case when x is a right child of y is easy. Hint: symmetric.
INSERTION
To insert a node into a BST
- find a leaf st the appropriate place and
- connect the node to the parent of the leaf.
TREE-INSERT (T, z)
y ← NIL
x ← root [T]
while x ≠ NIL do
y ← x
if key [z] < key[x]
then x ← left[x]
else x ← right[x]
p[z] ← y
if y = NIL
then root [T] ←z
else if key [z] < key [y]
then left [y] ← z
else right [y] ← z
Like other primitive operations on search trees, this algorithm begins at the root of the tree and traces a path downward. Clearly, it runs in O(h) time on a tree of height h.
Sorting
We can sort a given set of n numbers by first building a binary search tree containing these number by using TREE-INSERT (x) procedure repeatedly to insert the numbers one by one and then printing the numbers by an inorder tree walk.
Analysis
- Best-case running time
- Printing takes O(n) time and n insertion cost O(lg n) each (tree is balanced, half the insertions are at depth lg(n) -1). This gives the best-case running time O(n lg n).
-
- Worst-case running time
- Printing still takes O(n) time and n insertion costing O(n) each (tree is a single chain of nodes) is O(n2). The n insertion cost 1, 2, 3, . . . n, which is arithmetic sequence so it is n2/2.
Deletion
Removing a node from a BST is a bit more complex, since we do not want to create any "holes" in the tree. If the node has one child then the child is spliced to the parent of the node. If the node has two children then its successor has no left child; copy the successor into the node and delete the successor instead TREE-DELETE (T, z) removes the node pointed to by z from the tree T. IT returns a pointer to the node removed so that the node can be put on a free-node list, etc.
TREE-DELETE (T, z)
- if left [z] = NIL .OR. right[z] = NIL
- then y ← z
- else y ← TREE-SUCCESSOR (z)
- if left [y] ≠ NIL
- then x ← left[y]
- else x ← right [y]
- if x ≠ NIL
- then p[x] ← p[y]
- if p[y] = NIL
- then root [T] ← x
- else if y = left [p[y]]
- then left [p[y]] ← x
- else right [p[y]] ← x
- if y ≠ z
- then key [z] ← key [y]
- if y has other field, copy them, too
- return y
The procedure runs in O(h) time on a tree of height h. Implementationimport java.util.*;
public class BST <T extends Comparable<T>> implements Iterable<T>
{
public static void main(String[] args)
{
Integer[] a = {1,5,2,7,4};
BST<Integer> bst = new BST<Integer>();
for(Integer n : a) bst.insert(n);
bst.preOrderTraversal();
System.out.println();
//testing comparator
//build a mirror BST with a rule: Left > Parent > Right
//code for the comparator at the bottom of the file
bst = new BST<Integer>(new MyComp1());
for(Integer n : a) bst.insert(n);
bst.preOrderTraversal();
System.out.println();
bst.inOrderTraversal();
System.out.println();
for(Integer n : bst) System.out.print(n);
System.out.println();
System.out.println(bst);
//testing restoring a tree from two given traversals
bst.restore(new Integer[] {11,8,6,4,7,10,19,43,31,29,37,49},
new Integer[] {4,6,7,8,10,11,19,29,31,37,43,49});
bst.preOrderTraversal();
System.out.println();
bst.inOrderTraversal();
System.out.println();
//testing diameter
System.out.println("diameter = " + bst.diameter());
//testing width
System.out.println("width = " + bst.width());
}
private Node<T> root;
private Comparator<T> comparator;
public BST()
{
root = null;
comparator = null;
}
public BST(Comparator<T> comp)
{
root = null;
comparator = comp;
}
private int compare(T x, T y)
{
if(comparator == null) return x.compareTo(y);
else
return comparator.compare(x,y);
}
/*****************************************************
*
* INSERT
*
******************************************************/
public void insert(T data)
{
root = insert(root, data);
}
private Node<T> insert(Node<T> p, T toInsert)
{
if (p == null)
return new Node<T>(toInsert);
if (compare(toInsert, p.data) == 0)
return p;
if (compare(toInsert, p.data) < 0)
p.left = insert(p.left, toInsert);
else
p.right = insert(p.right, toInsert);
return p;
}
/*****************************************************
*
* SEARCH
*
******************************************************/
public boolean search(T toSearch)
{
return search(root, toSearch);
}
private boolean search(Node<T> p, T toSearch)
{
if (p == null)
return false;
else
if (compare(toSearch, p.data) == 0)
return true;
else
if (compare(toSearch, p.data) < 0)
return search(p.left, toSearch);
else
return search(p.right, toSearch);
}
/*****************************************************
*
* DELETE
*
******************************************************/
public void delete(T toDelete)
{
root = delete(root, toDelete);
}
private Node<T> delete(Node<T> p, T toDelete)
{
if (p == null) throw new RuntimeException("cannot delete.");
else
if (compare(toDelete, p.data) < 0)
p.left = delete (p.left, toDelete);
else
if (compare(toDelete, p.data) > 0)
p.right = delete (p.right, toDelete);
else
{
if (p.left == null) return p.right;
else
if (p.right == null) return p.left;
else
{
// get data from the rightmost node in the left subtree
p.data = retrieveData(p.left);
// delete the rightmost node in the left subtree
p.left = delete(p.left, p.data) ;
}
}
return p;
}
private T retrieveData(Node<T> p)
{
while (p.right != null) p = p.right;
return p.data;
}
/*************************************************
*
* toString
*
**************************************************/
public String toString()
{
StringBuffer sb = new StringBuffer();
for(T data : this) sb.append(data.toString());
return sb.toString();
}
/*************************************************
*
* TRAVERSAL
*
**************************************************/
public void preOrderTraversal()
{
preOrderHelper(root);
}
private void preOrderHelper(Node r)
{
if (r != null)
{
System.out.print(r+" ");
preOrderHelper(r.left);
preOrderHelper(r.right);
}
}
public void inOrderTraversal()
{
inOrderHelper(root);
}
private void inOrderHelper(Node r)
{
if (r != null)
{
inOrderHelper(r.left);
System.out.print(r+" ");
inOrderHelper(r.right);
}
}
/*************************************************
*
* CLONE
*
**************************************************/
public BST<T> clone()
{
BST<T> twin = null;
if(comparator == null)
twin = new BST<T>();
else
twin = new BST<T>(comparator);
twin.root = cloneHelper(root);
return twin;
}
private Node<T> cloneHelper(Node<T> p)
{
if(p == null)
return null;
else
return new Node<T>(p.data, cloneHelper(p.left), cloneHelper(p.right));
}
/*************************************************
*
* MISC
*
**************************************************/
public int height()
{
return height(root);
}
private int height(Node<T> p)
{
if(p == null) return -1;
else
return 1 + Math.max( height(p.left), height(p.right));
}
public int countLeaves()
{
return countLeaves(root);
}
private int countLeaves(Node<T> p)
{
if(p == null) return 0;
else
if(p.left == null && p.right == null) return 1;
else
return countLeaves(p.left) + countLeaves(p.right);
}
//This method restores a BST given preorder and inorder traversals
public void restore(T[] pre, T[] in)
{
root = restore(pre, 0, pre.length-1, in, 0, in.length-1);
}
private Node<T> restore(T[] pre, int preL, int preR, T[] in, int inL, int inR)
{
if(preL <= preR)
{
int count = 0;
//find the root in the inorder array
while(pre[preL] != in[inL + count]) count++;
Node<T> tmp = new Node<T>(pre[preL]);
tmp.left = restore(pre, preL+1, preL + count, in, inL, inL +count-1);
tmp.right = restore(pre, preL+count+1, preR, in, inL+count+1, inR);
return tmp;
}
else
return null;
}
//The width of a binary tree is the maximum number of elements on one level of the tree.
public int width()
{
int max = 0;
for(int k = 0; k <= height(); k++)
{
int tmp = width(root, k);
if(tmp > max) max = tmp;
}
return max;
}
//rerturns the number of node on a given level
public int width(Node<T> p, int depth)
{
if(p==null) return 0;
else
if(depth == 0) return 1;
else
return width(p.left, depth-1) + width(p.right, depth-1);
}
//The diameter of a tree is the number of nodes
//on the longest path between two leaves in the tree.
public int diameter()
{
return diameter(root);
}
private int diameter(Node<T> p)
{
if(p==null) return 0;
//the path goes through the root
int len1 = height(p.left) + height(p.right) +3;
//the path does not pass the root
int len2 = Math.max(diameter(p.left), diameter(p.right));
return Math.max(len1, len2);
}
/*****************************************************
*
* TREE ITERATOR
*
******************************************************/
public Iterator<T> iterator()
{
return new MyIterator();
}
//pre-order
private class MyIterator implements Iterator<T>
{
Stack<Node<T>> stk = new Stack<Node<T>>();
public MyIterator()
{
if(root != null) stk.push(root);
}
public boolean hasNext()
{
return !stk.isEmpty();
}
public T next()
{
Node<T> cur = stk.peek();
if(cur.left != null)
{
stk.push(cur.left);
}
else
{
Node<T> tmp = stk.pop();
while( tmp.right == null )
{
if(stk.isEmpty()) return cur.data;
tmp = stk.pop();
}
stk.push(tmp.right);
}
return cur.data;
}//end of next()
public void remove()
{
}
}//end of MyIterator
/*****************************************************
*
* the Node class
*
******************************************************/
private class Node<T>
{
private T data;
private Node<T> left, right;
public Node(T data, Node<T> l, Node<T> r)
{
left = l; right = r;
this.data = data;
}
public Node(T data)
{
this(data, null, null);
}
public String toString()
{
return data.toString();
}
} //end of Node
}//end of BST
class MyComp1 implements Comparator<Integer>
{
public int compare(Integer x, Integer y)
{
return y-x;
}
}
which is 
